The Time Value of Money (TVM) meaning is a core concept in finance based on the idea that money today is worth more than the same amount in the future. This guide addresses solving TVM problems using a timeline, which helps visualize cash flows and calculate values over time. We’ll also determine the payments needed to meet future financial goals.

For instance, you might want to figure out how much to save regularly to fund a child’s college tuition or calculate the monthly payments on a mortgage loan, which is related to the TVM meaning. In these cases, the process starts with gathering all the known information—such as interest rates, periods, and payment amounts. The appropriate formula is applied to find the missing value and solve the problem.

Planning for Retirement Savings

Suppose Joan intends to retire in 15 years and aims to accumulate at least $100,000 to fund a cruise worldwide. She wants to determine the equal end-of-year payments she must make over the next 15 years. The annual interest rate is 10%.

Key Variables

The key variables in this scenario include Joan’s future value of $100,000, which she will need at the end of year 15; the number of payments, which is 15; and the annual interest rate, which is 10%. Understanding the TVM meaning helps calculate the amount Joan must contribute at the end of each year to reach her goal. The objective is to calculate this amount.

When approaching financial problems, it’s helpful to visualize the information on a timeline.
In this case, the timeline consists of 15 equal end-of-year payments leading to a future value of $100,000.

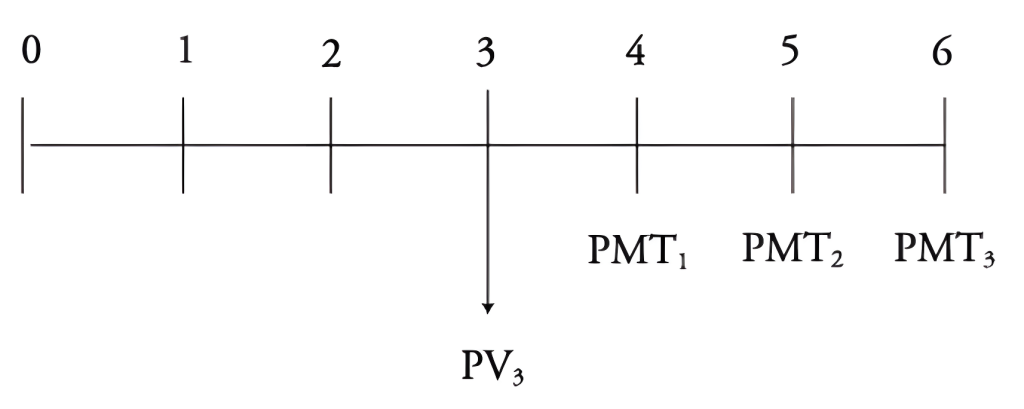
This cash flow structure might look familiar. Annuities involve equal, regular payments over a fixed number of periods. Here, we’ll use the future value formula for an ordinary annuity, solving for A, the annuity payment:

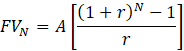
Let’s plug our known values into the formula:

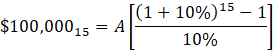
The present annuity factor is:

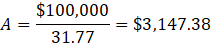
Next, divide $100,000 by 31.77 to find the required payment: $3,147.38. This is the amount Joan must save each year to reach her goal.  

Using Excel

Another way to reach the same result is by using Microsoft Excel. We’ll use the PMT function, which calculates periodic payments for a loan—but it also helps determine how much to save each period for a future goal.

Here’s how the function is set up:

  1. Rate – the interest rate per period: 10%
  2. Nper – total number of payments: 15
  3. PV – the present value: 0
  4. FV – the future value: -100,000 (entered as negative to get a positive result)
  5. Type (optional) – specifies when payments are made. (We’ll leave this blank, which defaults to end-of-period payments.)

The result: $3,147.38.

Consider Another Scenario

What if Joan thinks 15 years is too long and wants her dream vacation now? She could borrow $100,000 from a financial institution and repay it over 10 years with fixed end-of-year payments, demonstrating the TVM meaning. She wants to know the total of these payments.

Assume the interest rate stays at 10%. Let’s begin by mapping out the inputs on a timeline:

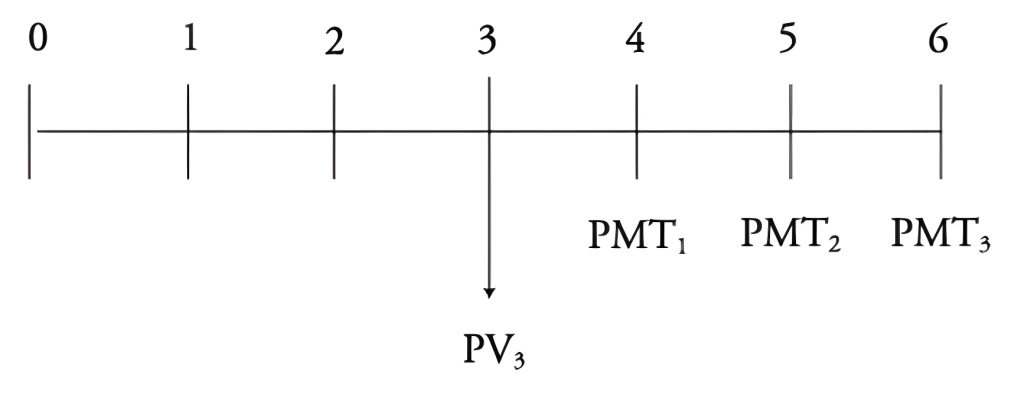
This time, the future value is unknown, but we know the present value, number of periods, and required rate of return. Since yearly payments are equal, the cash flow structure resembles an annuity.

We use the ordinary annuity formula because payments are made at the end of each year:

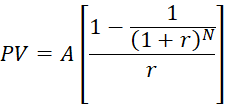
We can now easily plug in our known values:

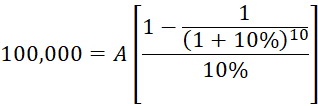
Starting with the bracketed terms: 1 minus 1 divided by (1 plus 10%) to the power of 10. Then divide the result by 10% to get 6.145:

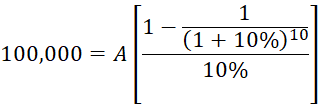
Most financial institutions require monthly rather than yearly payments. What would the monthly payment be for the same loan? We’d use the same method, incorporating TVM meaning into our calculations, but with a monthly interest rate. To get that, divide the 10% annual rate by 12, which gives about 0.83%.

Now, let’s plug the known values into the ordinary annuity formula:

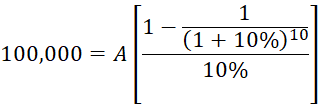
Starting with the bracketed terms: 1 minus 1 divided by (1 plus 0.83%) to the 120th power, the total number of periods. Then, divide the result by 0.83% to get 75.67.

Now divide $100,000 by 75.67 to find the monthly payment Joan must make for the next 10 years: $1,321.51:

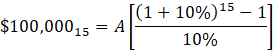
Verify the Result in Excel

  1. Use the PMT function.
  2. Enter the monthly interest rate:
    =RATE(12%) or simply 10%/12, which gives 0.83%.
  3. Set the number of periods to 120.
  4. Enter the present value (PV) as $100,000.
  5. Enter the future value (FV) as 0.
  6. Complete the formula and press Enter.

The result matches the previous calculation, confirming it’s correct.

TVM Meaning: Applying the Time Value of Money

Mastering the Time Value of Money and understanding the TVM meaning is essential for making informed financial decisions, whether saving for retirement, paying off a loan, or planning a large purchase. By identifying key variables and using formulas or Excel functions, you can confidently solve various financial problems. Whether calculating annual savings or monthly loan payments, visual tools like timelines and consistent methods ensure clarity and accuracy in your financial planning.

To harness the full potential of your financial analysis skills and take your career to the next level, consider joining the 365 Financial Analyst platform for comprehensive training and resources.

FREE SIGN UP