The Effective Annual Rate and Its Role in Compound Interest
The effective annual rate (EAR) reflects the true return on an investment by accounting for compounding periods within a year. Unlike stated interest rates, EAR provides a clearer picture of actual earnings, helping investors make more informed financial decisions.
Join over 2 million professionals who advanced their finance careers with 365. Learn from instructors who have worked at Morgan Stanley, HSBC, PwC, and Coca-Cola and master accounting, financial analysis, investment banking, financial modeling, and more.
Start for FreeBenjamin Franklin once wisely noted, “Money makes money. And the money that money makes, makes more money.” This insightful observation perfectly encapsulates the concept of compound interest and highlights why understanding effective annual rates (EARs) is critical.
Understanding Stated Annual Interest Rates
Financial institutions, such as banks, usually advertise their interest rates annually—known as stated annual interest rates. For instance, a bank may advertise a savings account with a yearly interest rate of 4% rather than breaking it down into quarterly increments. But these stated annual rates do not directly reflect what investors earn because they omit the impact of compounding interest.
The Concept of Effective Annual Rate (EAR)
To fully capture the benefits of compounding, we calculate the Effective Annual Rate (EAR). EAR adjusts the stated annual rate to include the effects of compounding periods within a year. The formula for calculating EAR is:
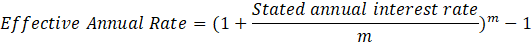
Here, two parameters are crucial:
- The Stated Annual Interest Rate is the annual nominal interest rate quoted by financial institutions.
- m is the number of compounding periods per year. Dividing the stated annual interest rate by m yields the periodic interest rate.
Practical Example
Suppose we invest $1,000 in a bank account for two years, with the bank offering an annual interest rate of 6%, compounded semi-annually. The compounding periods per year (m) equal 2; therefore, the periodic interest rate is 3% (6% ÷ 2).
Applying the EAR formula:
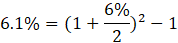
In this example, the EAR is approximately 6.1%—illustrating that compounding increases the actual earned interest compared to the stated annual rate.
Comparing Different Compounding Frequencies
Let’s modify the previous scenario by changing the compounding frequency from semi-annual to monthly. With monthly compounding, we now have m = 12, and the periodic interest rate becomes 0.5% (6% ÷ 12).
Applying the EAR formula again:
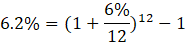
Notice the upward trend? The EAR increases as compounding frequency increases. Monthly compounding yields a higher EAR (6.2%) than semi-annual compounding (6.1%).
Key Insight
The key takeaway is straightforward: the greater the compounding frequency, the higher the effective annual interest rate. This concept is crucial for investors because it highlights the advantage of choosing financial products that compound more frequently.
Benjamin Franklin’s quote profoundly emphasizes the principle behind compound interest: “Money makes money, and the money that money makes, makes more money.”
Effective Annual Rate and Smarter Financial Decisions
Understanding and accurately calculating the Effective Annual Rate helps investors evaluate financial products. It enables better financial decisions that maximize earnings through the powerful mechanism of compounding.
If you’re ready to apply these insights and enhance your financial skills, the 365 Financial Analyst platform offers the perfect next step with structured learning and real-world applications.
