Put-Call Parity for European Options
Put-call parity is a foundational concept in options pricing that defines the relationship between European call and put options with the same strike price and expiration. This principle ensures pricing consistency in efficient markets and provides the groundwork for constructing synthetic positions and advanced trading strategies.
Join over 2 million professionals who advanced their finance careers with 365. Learn from instructors who have worked at Morgan Stanley, HSBC, PwC, and Coca-Cola and master accounting, financial analysis, investment banking, financial modeling, and more.
Start for FreePut-call parity is a fundamental principle in the pricing of European options. To understand it, it helps first to consider the meaning of “parity”—a term that traces back to Late Latin, which referred to “equality of rank or status.” This sense of balance remains central to put-call parity, which describes a specific, predictable relationship between the prices of European call and put options with the same strike price and expiration date.
Put-Call Parity
In modern finance, put-call parity is a fundamental concept that outlines the relationship between European call options and European put options with the same strike price and expiration date. This principle allows us to understand how different financial instruments can be combined to replicate each other’s payoff under the assumption that there is no arbitrage in the market.
Core Components of the Parity Equation
Put-call parity is built upon four instruments:
- Call option
- Put option
- Zero-coupon bond
- Underlying assets associated with the options
The equation expresses the central idea: Fiduciary Call = Protective Put. These are two distinct portfolios that produce the same outcome at maturity.
A fiduciary call comprises a call option and a zero-coupon bond, while a protective put combines a long-put option and the underlying asset. The term “protective” reflects the nature of this strategy—it limits downside risk by allowing the investor to sell the asset at the strike price, even if the market value drops.
Why They Must Be Equal
Since both portfolios derive their value from the same underlying asset and have the same strike price, the no-arbitrage principle dictates that they must be valued equally in efficient markets. If they weren’t, arbitrage opportunities would exist—allowing traders to earn risk-free profits and eventually eliminate the price difference.
Variables and Notation
To express this mathematically, we use the following notations:

Under the no-arbitrage principle, the relationship must satisfy:
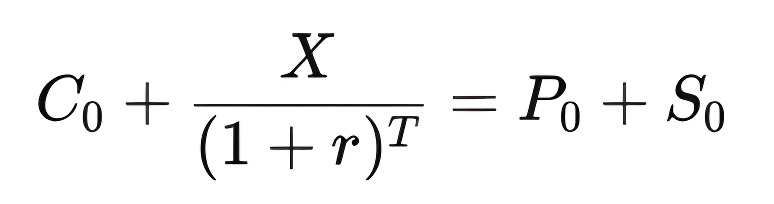
This confirms that the value of the fiduciary call equals that of the protective put.
Case Analysis: Two Scenarios
To prove this relationship, let’s examine two possible outcomes at expiration.
Scenario 1
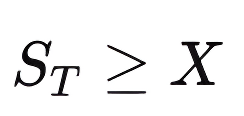
When the market price of the asset at maturity is greater than or equal to the strike price:
The call is exercised:
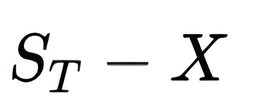
The put expires worthless.
Portfolio outcomes
Fiduciary Call:
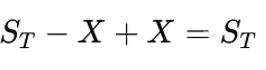
Protective Put:
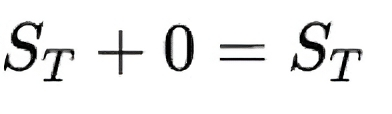
Scenario 2
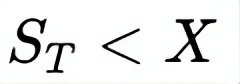
When the asset’s price is below the strike price:
The put is exercised:
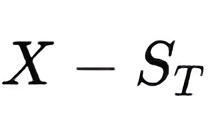
The call expires worthless.
Portfolio outcomes
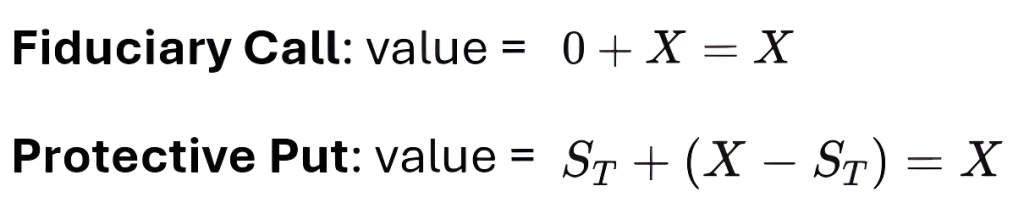
In both scenarios, the portfolios have identical values at expiration, confirming the put-call parity principle.
Practical Implications
The significance of this principle goes beyond theoretical proof. It allows investors to construct synthetic positions—replicating the payoff of one instrument using others. For example, combining a protective put with a short position in a risk-free bond can effectively create a synthetic European call option. This flexibility is vital for hedging strategies and speculative positions because it offers multiple pathways to achieve desired financial outcomes.
Looking Ahead: Using Parity for Strategy
This leads to a deeper question: How can we combine a forward contract with options to replicate other financial assets or portfolios? The logic behind put-call parity provides a foundation for answering such questions and constructing even more sophisticated financial products.
Put-Call–Forward Parity
Now that you understand the basic put-call parity, let’s move on to the concept of put-call–forward parity for European options. This parity version involves combining an asset with a short position in a forward contract on that asset, resulting in a payoff identical to a risk-free bond. In simple terms, this is a method of perfect risk hedging.
Mathematical Expression of Put-Call–Forward Parity
The put-call–forward parity can be mathematically expressed to show that when the formula is rearranged, an asset equals a long position in a forward contract plus a risk-free bond. This relationship is crucial because it allows the substitution of positions involving forwards and bonds for direct ownership of an asset.
Extending to Protective Put
Now, let’s take the asset’s value from this formula and plug it into the protective put formula we discussed earlier with regular put-call parity.
- On the left-hand side, we now have a protective put, which consists of the asset plus a put option on that asset:
Protective Put = Asset + Put Option
- On the right-hand side, we have a long forward contract plus a risk-free bond plus a put option:
Long Forward Contract + Risk-Free Bond + Put Option
It’s essential to note that the underlying asset remains consistent across all derivative contracts involved in this setup.
Proving the Parity with Scenarios
Let’s analyze two market scenarios to confirm that the two sides are truly equal.
- Scenario 1: The market price of assets is less than the exercise price.
When the market price of the asset is lower than the strike price at the contract’s expiration:- By substituting the known parameters into both sides of the equation, we find that each side results in a value of X (the strike price).
- This indicates that when the asset’s market price is below the exercise price, both portfolios will be worth exactly the strike price.
- Scenario 2: The market price of assets is greater than or equal to the exercise price.
In this case, when the asset’s market price meets or exceeds the strike price:- Substituting into the formula shows that both sides now equal (the asset price at maturity).
In both scenarios, the left-hand side and the right-hand side of the equation are identical. The two sides match perfectly under all conditions. This result is put-call–forward parity. It extends the original put-call parity logic to markets involving forward contracts—efficiently providing investors with another robust tool for hedging and structuring portfolios.
Bridging Put-Call Parity Principles for Strategic Insight
The concepts of put-call parity and put-call–forward parity form a crucial foundation in understanding and navigating the pricing and relationships of European options. Together, they demonstrate how seemingly distinct financial instruments (calls, puts, bonds, forwards, and the underlying asset) can be structured to create equivalent payoffs under the no-arbitrage condition.
By confirming parity across various market scenarios, investors gain powerful tools for building synthetic positions, managing risk, and designing strategic portfolios precisely. This parity framework reinforces theoretical consistency and empowers practical decision-making in modern financial markets.
To deepen your understanding of concepts like this and gain hands-on experience, consider joining the 365 Financial Analyst platform, where practical training meets expert instruction.
