Time Value of Money Problems
Understanding the time value of money problems is essential for evaluating investments and financial decisions. This guide explains how different compounding frequencies and the effective annual rate affect present and future values, using clear, practical examples.
Join over 2 million professionals who advanced their finance careers with 365. Learn from instructors who have worked at Morgan Stanley, HSBC, PwC, and Coca-Cola and master accounting, financial analysis, investment banking, financial modeling, and more.
Start for FreeGrasping the time value of money (TVM) is essential in finance because it helps evaluate money’s worth at different times. This guide focuses on solving the time value of money problems—particularly how varying compounding frequencies, such as annual, semi-annual, quarterly, and monthly, affect the value of money over time. To illustrate the practical application of these principles, let’s calculate the future and present value of Melissa’s investment.
Future Value with Quarterly Compounding
Melissa is considering investing $3,000 in a deposit for two years at a bank that offers a 6% annual interest rate with quarterly compounding. She wants to determine the future value of her investment.
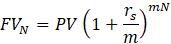
- Calculate the total number of compounding periods. Since the bank compounds interest quarterly over two years, we multiply four yearly periods by 2, resulting in 8 total periods.
- Determine the periodic interest rate by dividing Melissa’s annual interest rate of 6% by the four quarterly periods, giving us 1.5% per period.
- To find the future value of her investment, we multiply her initial principal of $3,000 by (1 + 0.015), raised to the power of 8, which calculates to $3,379.48.
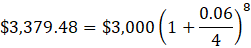
Verifying with the Effective Annual Rate (EAR)
Alternatively, we can calculate the effective annual rate (EAR) and then determine the future value of the investment. This time value of money problem involves raising 1.015 to the power of 4 and then subtracting 1, we find an EAR of 6.1%. Using this rate, Melissa’s $3,000 investment will grow 6.1% annually over two years, achieving the same result: $3,379.48.
To confirm this, we multiply $3,000 by (1 + 0.061), raised to the power of 2 to find the same future value.
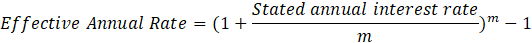

Present Value with Monthly Compounding
Let’s calculate the present value of a certificate of deposit (CD) that will pay $10,000 after three years, using a 12% interest rate with monthly compounding. Initially, it may seem that we don’t know how to calculate the present value. But we can leverage our understanding of the future value formula by rearranging it to determine the present value. By doing so, we can determine how much we would need to invest today to receive $10,000 in three years under these conditions.
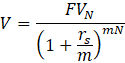
The present value is calculated by dividing the future value by (1 plus the periodic interest rate) raised to the power of the total number of compounding periods—where m represents the number of compounding periods per year, and N is the total number of years.
Now, we have all the information needed to calculate the present value of the deposit. We know the certificate of deposit will mature to $10,000 in three years, which is our future value.
With monthly compounding, the total number of compounding periods over three years is 36 (12 per year multiplied by 3 years). The periodic interest rate is 1%, calculated by dividing the annual rate by the number of compounding periods per year. This time value of money problem requires calculating $10,000 divided by (1 + 1%) raised to the power of 36, resulting in a present value of $6,989.25.

Using EAR for Present Value Calculations
Alternatively, we could calculate using the EAR to achieve the same result. By raising 1.01 to the power of 12 and subtracting 1, we find an EAR of 12.7%. We then discount the $10,000 by (1.127) raised to the power of 3, yielding a present value of $6,989.25.
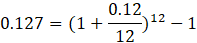
Note that when there are no multiple compounding periods per year, the formula for calculating present value simplifies to the following equation:
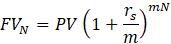
As you can see, m is equal to 1—simplifying the application of the formula significantly.
Solving Time Value of Money Problems
Understanding the calculations for both present and future values of investments, using different compounding frequencies and rates, is crucial in financial planning. Each scenario represents a time value of money problem, where the value of money changes depending on time and interest rates. By mastering these formulas, we can make informed decisions about investments like certificates of deposit. We’ve seen how adjusting the compounding frequency or using the effective annual rate can impact the outcomes of these calculations. This knowledge enhances our financial acumen and empowers us to manage better and grow our investments over time.
To continue building on this foundation and further enhance your financial analysis skills, consider joining the 365 Financial Analyst platform—where you can access comprehensive resources and expert guidance tailored to your financial education needs.
